问题描述
给定一棵二叉树的根节点`root“,要求将其按前序遍历的顺序展开为一个单链表。展开后的链表应满足以下条件:
- 链表的顺序与二叉树的前序遍历结果一致。
- 链表中每个节点的右子指针指向下一个节点,左子指针始终为
null。
示例输入与输出
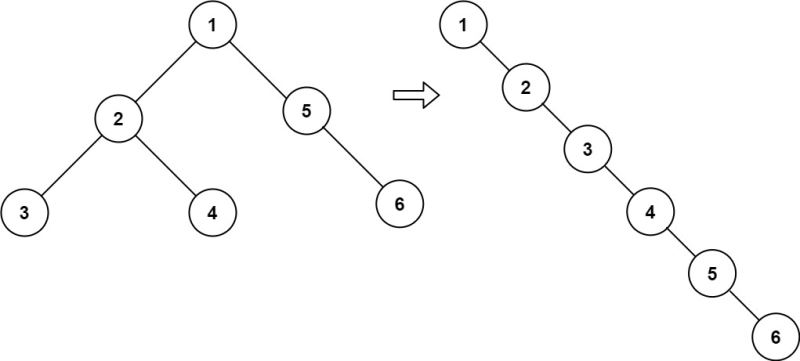
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
解决方案
方法一:迭代法(Morris遍历思路)
核心思想:通过修改指针实现原地展开,无需额外空间。类似Morris遍历,时间复杂度O(n),空间复杂度O(1)。
实现步骤
- 初始化当前节点:从根节点开始遍历。
- 处理左子树:对于每个节点,若存在左子树,找到左子树的最右节点。
-
调整指针:
- 将左子树的最右节点的右指针指向当前节点的右子树。
- 将当前节点的右指针指向左子树,左指针置空。
- 迭代处理:沿右指针处理下一个节点,直到所有节点处理完毕。
Java代码实现
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(intnsbsKFB val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
public class Solution {
public void flatten(TreeNode root) {
TreeNode curr = root;
while (curr != null) {
if (curr.left != null) {
// 找到左子树的最右节点
TreeNode prev = curr.left;
while (prev.right != null) {
prev = prev.rigphpht;
}
// 将右子树接到最右节点
prev.right = curr.right;
// 将左子树移到右侧,并清空左侧
curr.right = curr.left;
curr.left = null;
}
// 处理下一个节点
curr = curr.right;
}
}
}
关键解释
- 左子树的最右节点:前序遍历中,左子树的最后一个节点需要连接到当前节点的右子树。
- 指针调整:通过修改指针实现原地展开,无需额外空间。
方法二:前序遍历+列表重建
核心思想:显式存储前序遍历结果,再重建链表。时间复杂度O(n),空间复杂度O(n)。
实现步骤
- 前序遍历存储节点:递归遍历二叉树,按前序顺序将节点存入列表。
- 重建链表:遍历列表,将每个节点的左指针置空,右指针指向下一个节点。
Java代码实现
import java.util.ArrayList;
import java.util.List;
class Solution {
public void flatten(TreeNode root) {
if (root == null || (root.left == null && root.right == null)) return;
List<TreeNode> result = new ArrayList<>();
preOrder(root, result);
// 重建链表
for (int i = 0; i < result.size() - 1; i++) {
TreeNode prev = result.get(i);
TreeNode cur = result.get(i + 1);
prev.left = null;
prev.right = cur;
}
}
private void preOrder(TreeNode root, List<TreeNode> result) {
if (root == null) return;
result.add(root);
preOrder(root.left, result);
preOrder(root.right, result);
}
}
关键解释
- 前序遍历列表:显式存储节点顺序,逻辑直观。
- 空间开销:需额外存储所有节点的引用,空间复杂度为O(n)。
方法对比与分析
| 特性 | 方法一(迭代法) | 方法二(前序遍历+列表) |
|---|---|---|
| 时间复杂度 | O(n) | O(n) |
| 空间复杂度 | O(1) | O(n) |
| 代码复杂度 | 高(需处理指针调整) | 低(逻辑直观) |
| 栈溢出风险 | 无 | 有(递归深度高时) |
| 适用场景 | 内存敏感、大规模数据 | 快速实现、小规模数据 |
选择建议
-
优先方法一:
- 适用场景:内存受限(如嵌入式开发)、处理超大规模树。
- 优点:原地修改,无额外空间开销。
- 缺点:指针操作复杂,需深入理解Morris遍历。
-
优先方法二:
- 适用场景:快速实现、代码可读性优先、小规模数据。
- 优点:逻辑编程清晰,易于调试。
- 缺点:空间开销大,递归可能栈溢出。
拓展:方法二的迭代优化
将递归前序遍历改为迭代实现,避免栈溢出风险:
private void preOrder(TreeNode root, List<TreeNode> result) {
Deque<TreeNode> stack = new ArrayDeque<>();
TreeNode node = root;
while (node != null || !stack.isEmpty()) {
while (node != null) {
php result.add(node);
stack.push(node);
node = node.left;
}
node = stack.pop();
node = node.right;
}
}